Parabolic cylinder function
In mathematics, the parabolic cylinder functions are special functions defined as solutions to the differential equation
This equation is found, for example, when the technique of separation of variables is used on differential equations which are expressed in parabolic cylindrical coordinates.
The above equation may be brought into two distinct forms (A) and (B) by completing the square and rescaling z, called H. F. Weber's equations (Weber 1869):
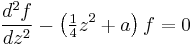 (A)
(A)
and
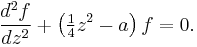 (B)
(B)
If
is a solution, then so are
If
is a solution of equation (A), then
is a solution of (B), and, by symmetry,
are also solutions of (B).
Solutions
There are independent even and odd solutions of the form (A). These are given by (following the notation of Abramowitz and Stegun (1965)):
and
where 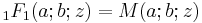 is the confluent hypergeometric function.
is the confluent hypergeometric function.
Other pairs of independent solutions may be formed from linear combinations of the above solutions (see Abramowitz and Stegun). One such pair is based upon their behavior at infinity:
where
The function U(a, z) approaches zero for large values of |z| and |arg(z)| < π/2, while V(a, z) diverges for large values of positive real z .
and
For half-integer values of a, these (that is, U and V) can be re-expressed in terms of Hermite polynomials; alternatively, they can also be expressed in terms of Bessel functions.
The functions U and V can also be related to the functions Dp(x) (a notation dating back to Whittaker (1902)) that are themselves sometimes called parabolic cylinder functions (see Abramowitz and Stegun (1965)):
References
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 19", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 686, ISBN 978-0486612720, MR0167642, http://www.math.sfu.ca/~cbm/aands/page_686.htm.
- Rozov, N.Kh. (2001), "Weber equation", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=W/w097310
- Temme, N. M. (2010), "Parabolic cylinder function", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248, http://dlmf.nist.gov/12
- Weber, H.F. (1869) "Ueber die Integration der partiellen Differentialgleichung
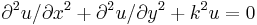 ". Math. Ann. , 1, 1–36
". Math. Ann. , 1, 1–36 - Whittaker, E.T. (1902) "On the functions associated with the parabolic cylinder in harmonic analysis" Proc. London Math. Soc.35, 417–427.
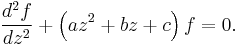
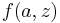
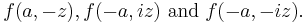
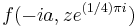
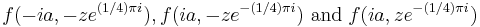
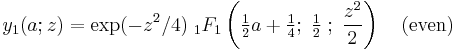
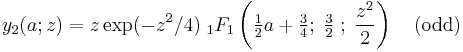
![U(a,z)=\frac{1}{2^\xi\sqrt{\pi}}
\left[
\cos(\xi\pi)\Gamma(1/2-\xi)\,y_1(a,z)
-\sqrt{2}\sin(\xi\pi)\Gamma(1-\xi)\,y_2(a,z)
\right]](/2012-wikipedia_en_all_nopic_01_2012/I/f05ce58956205a33d5c0219ae8c9419b.png)
![V(a,z)=\frac{1}{2^\xi\sqrt{\pi}\Gamma[1/2-a]}
\left[
\sin(\xi\pi)\Gamma(1/2-\xi)\,y_1(a,z)
%2B\sqrt{2}\cos(\xi\pi)\Gamma(1-\xi)\,y_2(a,z)
\right]](/2012-wikipedia_en_all_nopic_01_2012/I/b0bb0c6dcfbe955e032bb439a42acc61.png)
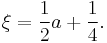
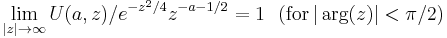
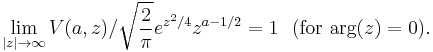
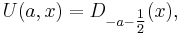
![V(a,x)=\frac{\Gamma(\tfrac12%2Ba)}{\pi}[\sin( \pi a) D_{-a-\tfrac12}(x)%2BD_{-a-\tfrac12}(-x)] .](/2012-wikipedia_en_all_nopic_01_2012/I/20299e328e948a6d06c39a8698d6fb8e.png)